3 Lines in a Square
(based on a submission from Paul Cleary)
Six points A,B,C,D,E,F with integer coordinates are chosen on the boundary of an N×N square,
with integer N≤100. The 3 line segments AB, CD and EF are drawn forming a triangle that encloses
the center point P of the square. For what value of N and points A,B,C,D,E,F
is the area of this triangle smallest?
Solved by: Arthur Vause, Ender Aktulga
## 3 Lines in a Square #2
(based on a submission from Paul Cleary)
Six points A,B,C,D,E,F with integer coordinates are chosen on the boundary of an N×N square,
with integer N≤100. Three line segments AB, CD and EF are drawn to form a triangle.
For what value of N and points A,B,C,D,E,F is the area of this triangle smallest?
Solved by: Arthur Vause
## Nested Rectangles
There are 3 rectangles, A, B and C all with integer sides.
Rectangle B can be nested inside of A so that each vertex of B lies on an edge of A,
with the distance from that vertex of B to the closest vertex of A being an integer.
In the same way, rectangle C can be nested inside A,
and rectangle C can also be nested inside B.
What is the smallest possible area for rectangle A?
Solve two cases, when all of the rectangles are squares, and when none
of the rectangles are squares.
All Squares: Claudio Baiocchi, Arthur Vause
No Squares: Arthur Vause
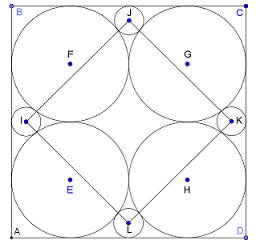
Circles in a Square
(based on a submission from Paul Cleary)
Four equal circles E, F, G and H are inscribed in a unit square ABCD so that each circle is
tangent to two sides of the square and to two of the other circles.
Four smaller circles I, J, K and L are drawn so that each is tangent to a side of the square
and two of the larger circles, as shown.
How large is the square IJKL?
Solved by: Arthur Vause, P.M.A. Hakeem, Fotos Fotiadis, Claudio Baiocchi, Ritwik Chaudhuri,
Mark Rickert, Ionut-Zaharia Chirila, Amogh Keni, Ender Aktulga, Naim Uygun
|
|
* Equal Circles
(contributed by Paul Cleary)
ABC is a right triangle with legs a and b and hypotenuse c.
Two circles of radius r are placed inside the triangle, the first tangent to a and c,
the second tangent to b and c, and both circles externally tangent to each other.
What is the smallest possible area of the triangle if a, b, c and r are distinct integers?
Solved by: P.M.A. Hakeem, Nick McGrath, Fotos Fotiadis, Ahmet Saracoglu,
Ahsen Canat, Claudio Baiocchi, Naim Uygun, Mark Rickert, Ionut-Zaharia Chirila,
Ender Aktulga
* Equal Circles #2
(contributed by Paul Cleary)
ABC is a right triangle with legs a and b and hypotenuse c.
Two circles of radius r are placed inside the triangle, the first tangent to a and c,
the second tangent to b and c, and both circles externally tangent to each other.
Draw a third circle of radius s tangent externally to the first two circles, and
to the hypotenuse.
What is the smallest possible radius of the third circle if a, b, c, r and s are distinct integers?
Solved by: P.M.A. Hakeem, Nick McGrath, Ahsen Canat, Fotos Fotiadis,
Claudio Baiocchi, Mark Rickert, Ionut-Zaharia Chirila, Ender Aktulga, Naim Uygun
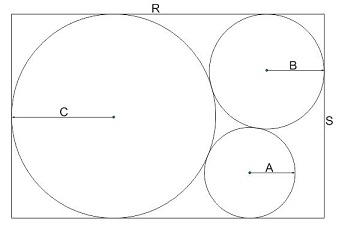
* Boxed Circles
(contributed by Paul Cleary)
Three circles of radius A, B and C are mutually tangent externally, and enclosed
in a rectangle whose sides are R and S, with 6 points of tangency, as shown at right.
Find the values of R and S as functions of A and B only.
Solved by: Ahsen Canat, P.M.A. Hakeem, Arthur Vause, Fotos Fotiadis,
Claudio Baiocchi, Tim Joseph Clark, Naim Uygun, Mark Rickert, Ionut-Zaharia Chirila,
Ender Aktulga, Ahmet Saracoglu, Amogh Keni, Kenneth Bennett
|
|
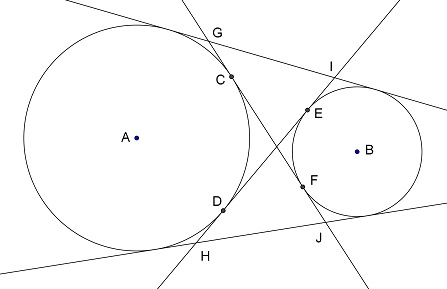
4 Tangents
(contributed by Paul Cleary)
Four tangent lines have been drawn to two non-overlapping circles A and B.
The two interior tangents, which intersect the line segment AB, meet the circles
at C, D, E and F, as shown, and intersect the two exterior tangents
at G, H, I and J.
Prove that segments CF, DE, GI and HJ are all equal.
Solved by: Arthur Vause, Amogh Keni, Ahmet Saracoglu, Ionut-Zaharia Chirila
|
|
Area : Perimeter
(contributed by Paul Cleary)
The triangle 5,12,13 has an area A=30 and a perimeter P=30, so A/P is 1.
The triangle 9,75,78 has an area A=324 and a perimeter P=162, so A/P is 2.
Find the smallest and largest integer-sided triangles where A/P is 10.
Solved by: Nick McGrath, P.M.A. Hakeem, Fotos Fotiadis, Arthur Vause,
Claudio Baiocchi, Ionut-Zaharia Chirila, Ender Aktulga, Kaustuv Sengupta
Heronian Triangles
A Heronian triangle has integer sides and integer area.
Find two Heronian triangles (x,y,z) and (x+c,y+c,z+c) for the smallest
possible value of c>0.
Solved by: Nick McGrath, Fotos Fotiadis, Mark Rickert, P.M.A. Hakeem,
Paul Cleary, Arthur Vause, Naim Uygun, Ionut-Zaharia Chirila, Ender Aktulga
Square Heronian
(contributed by Lee Morgenstern)
A Heronian triangle has integer sides and integer area.
A primitive Heronian triangle has sides with gcd(A,B,C)=1.
Find a primitive Heronian triangle where all 3 sides are squares.
[When this problem was first posted, only one solution was known.
Extra credit for anyone who finds a second solution.]
Solved by: Arthur Vause, Paul Cleary, P.M.A. Hakeem,
Ionut-Zaharia Chirila, Ender Aktulga
Extra Credit: Naim Uygun (2 solutions), Kaustuv Sengupta (2 solutions)
Power Heronian
(contributed by Paul Cleary)
A Heronian triangle has integer sides and integer area.
Find two Heronian triangles which have one side in common,
where the other two sides of each are a square and a cube.
Solved by: Naim Uygun (found a triple),
Ender Aktulga (10 pairs), P.M.A. Hakeem (2 pairs), Kaustuv Sengupta (1 pair),
Ionut-Zaharia Chirila (1 pair)
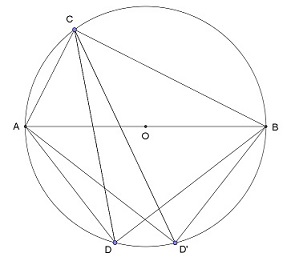
Cyclic Quadrilaterals
(contributed by Paul Cleary)
Let O be a circle with diameter AB having integer length.
Let C and D be points on the circumference such that ACB and ADB are integer
Pythagorean triangles.
Choose D' so that AD=BD' and BD=AD'.
Then ACBD and ACBD' are cyclic quadrilaterals with diagonals AB, CD and CD'.
What is the smallest case for which the lengths of AB, CD and CD' are consecutive integers
in some order?
Solved by: Arthur Vause, P.M.A. Hakeem, Fotos Fotiadis, Ionut-Zaharia Chirila,
Naim Uygun, Ender Aktulga
|
|
The Folding Ruler
I own one of those folding rulers where each segment is exactly 1 foot long.
While playing with the open ruler I formed it into a triangle. Then I
refolded it into a second triangle with double the area.
What is the smallest possible length of the ruler?
What if the second triangle has 3 times the area?
Solved by: Lee Morgenstern, Nick McGrath, P.M.A. Hakeem, Paul Cleary,
Mark Rickert, Claudio Baiocchi, Ender Aktulga, Naim Uygun, Kaustuv Sengupta
The Folding Ruler #2
I own one of those folding rulers where each segment is exactly 1 foot long.
While playing with the open ruler I formed it into a triangle.
Then I refolded it into a second triangle with double the area.
Next I refolded it into a third triangle with triple the area.
What is the smallest possible length of the ruler?
Solved by: Nick McGrath, Lee Morgenstern, P.M.A. Hakeem, Paul Cleary,
Mark Rickert, Claudio Baiocchi, Naim Uygun, Ender Aktulga, Kaustuv Sengupta
Triangle Ratios
For what rational numbers a/b is it possible to find two triangles
with integer sides whose areas are in the ratio a:b?
Solved by: Lee Morgenstern, P.M.A. Hakeem
Bowtie
Two line segments AB and CD intersect at E. Is it possible for the
lengths of the 6 line segments AD, AE, BC, BE, CE and DE to be
consecutive integers (in any order)?
Solved by: Lee Morgenstern, Fotos Fotiadis, Arthur Vause, P.M.A. Hakeem,
Ender Aktulga
Pie
It is easy to cut a circular pie into 7 pieces using 3 straight cuts.
How should the cuts be made so that the 7 pieces are as even as possible?
(That is, the ratio between the largest and smallest piece should be
minimal.)
Solved by: Fotos Fotiadis, Paul Cleary, Ender Atulga
Make A Square
What is the smallest number of pieces that can be assembled into a
square in 2 distinct ways? 3 distinct ways?
Solutions where the pieces, or the square, are merely rotated or
reflected (turned over) will not be considered distinct.
Solved by: Lee Morgenstern, Nick McGrath
In the following Pythagorean Triangle puzzles the sides
of each triangle are always given in ascending order.
Pythagorean Triangles #1A
Find two Pythagorean right triangles A,B,C and D,E,F
such that A+D is a square, B+E is a square, and C+F is a square.
If this is impossible, find the nearest miss.
Solved by: Lee Morgenstern, Paul Cleary, P.M.A. Hakeem, Naim Uygun,
Ender Aktulga
Pythagorean Triangles #1B (Contributed by Naim Uygun)
Find two Pythagorean right triangles A,B,C and D,E,F
such that A+D is a triangular number, B+E is a triangular number, and C+F is a triangular number.
Triangular numbers are numbers of the form N(N+1)/2, such as 1, 3, 6, 10, 15, ... .
Solved by: Paul Cleary, P.M.A. Hakeem, Ender Aktulga,
Kaustuv Sengupta (28 pairs)
Pythagorean Triangles #1C
Find two Pythagorean right triangles with sides A,B,C and D,E,F
such that A+D is a cube, B+E is a cube, and C+F is a cube.
Solved by: Lee Morgenstern, Paul Cleary, P.M.A. Hakeem
Pythagorean Triangles #1D
Find two Pythagorean right triangles A,B,C and D,E,F
such that A+D is a cube, B+E is a sixth power, and C+F is a ninth power.
Solved by: Lee Morgenstern, Paul Cleary
Pythagorean Triangles #2
(contributed by Lee Morgenstern)
Find two Pythagorean right triangles A,B,C and D,E,F
such that A=D and B=F. If that is impossible, then find
a pair such that A=D and abs(B-F) is minimum.
Solved by: Paul Cleary, P.M.A. Hakeem
Pythagorean Triangles #3
(contributed by Lee Morgenstern)
Find two Pythagorean right triangles A,B,C and D,E,F
such that A=D and B=2E. If that is impossible, then find
a pair such that A=D and abs(B-2E) is minimum.
Solved by: Paul Cleary, P.M.A. Hakeem
Pythagorean Triangles #4
(contributed by Lee Morgenstern)
Find two Pythagorean right triangles A,B,C and D,E,F
such that C=D+E and F=A-B. If this is impossible, find
the triangles that come closest.
Solved by: P.M.A. Hakeem, Paul Cleary
## Three Triangles
Find three Pythagorean right triangles having the same hypotenuse, such
that the total area of the first two equals the area of the third,
or prove that this is impossible.
## Packing a Cube
You wish to pack a hollow cube with N spheres so that the least possible
space is left over.
Either (1) prove that this is achieved by the greedy algorithm, namely
at each step you insert the largest possible sphere that will fit,
or (2) find the smallest N for which a tighter packing is possible.
Euler Lines
Let ABC be a general triangle and let O be its circumscribed circle.
Let DEF be a second general triangle inscribed in O. Prove that the
Euler line of ABC and the Euler line of DEF intersect at O.
Solved by: Nick McGrath, Fotos Fotiadis, P.M.A. Hakeem, Amogh Keni,
Abhay Menon
Point on Circumcircle
(contributed by Fotos Fotiadis)
ABC is a triangle whose smallest angle is A. K is a point on the arc BC
of the circumcircle. The perpendicular bisectors of AB and AC intersect
the line AK at L and M, respectively. The lines BL and CM intersect at T.
Prove that BT+CT=AK.
Solved by: Arthur Vause, Amogh Keni, Ionut-Zaharia Chirila
Consecutive Distances
(contributed by Denis Borris )
Point P is located inside triangle ABC. The lines PA, PB and PC are drawn
and extended to meet the opposite sides at D, E and F.
(1) Is it possible for the lengths of PA, PB and PC to be consecutive integers,
and the lengths of PD, PE and PF also to be consecutive integers, in some order?
If so, what is the smallest case (smallest area)?
(2) Is it possible for all 6 of those lengths to be consecutive integers?
If so, what is the smallest case (smallest area)?
A Point in a Triangle
(contributed by Denis Borris )
A point P is located inside an equilateral triangle with integer side k,
such that its distances to the 3 vertices are integers a,b,c. What is the
smallest possible value of a? Of k?
Solved by: Jean Jacquelin, Fotos Fotiadis, P.M.A. Hakeem, Paul Cleary,
Ionut-Zaharia Chirila, Naim Uygun, Ender Aktulga
Two Points in a Triangle
(contributed by Denis Borris )
Points P and Q are located inside an isosceles triangle with integer sides,
such that their distances to the 3 vertices and the length PQ
are distinct integers. What is the smallest case (smallest length PQ)?
Solved by: Jean Jacquelin, P.M.A. Hakeem, Paul Cleary, Ahsen Canat,
Naim Uygun, Ender Aktulga
Two Points in a Triangle #2
(contributed by Naim Uygun )
Points P and Q are located inside a scalene triangle with integer sides,
such that their distances to the 3 vertices and the length PQ
are distinct integers. What is the smallest case (smallest length PQ)?
Solved by: Ender Aktulga
* Three Points in a Triangle
Three points P, Q and R are located interior to a triangle ABC with all 15 distances
distinct integers. What is the smallest case?
Solved by: Jean Jacquelin, Ahsen Canat, Ahmet Saracoglu, Arthur Vause
** Triangle Within a Triangle
A triangle DEF is located interior to triangle ABC with all 15 distances
distinct integers. What is the smallest case (smallest area of ABC)?
Solved by: Jean Jacquelin, Ahsen Canat, Ahmet Saracoglu, Arthur Vause
Overlap #1
A circle and a triangle overlap so that the circle cuts each side
of the triangle into 3 line segments. What is the smallest
possible radius of the circle if the 9 line segments all have
distinct integer lengths?
Solved by: Nick McGrath, Fotos Fotiadis, P.M.A. Hakeem, Naim Uygun,
Ender Aktulga
Overlap #2
A circle and a triangle overlap so that the circle cuts each side
of the triangle into 3 line segments. What is the smallest possible
radius of the circle if the 9 line segments and the radius of the
circle all have distinct integer lengths?
Solved by: Nick McGrath, Ender Aktulga, Naim Uygun
* Overlap #3
A circle and a triangle overlap so that the center of the circle is
at the barycenter of the triangle (where the medians intersect), and
the circle cuts each side of the triangle into 3 line segments.
What is the smallest possible radius of the circle if the 9 line segments
all have distinct integer lengths?
Solved by: Jean Jacquelin, Ahsen Canat, Ender Aktulga
* Overlap #4 (Contributed by Naim Uygun)
A circle and a scalene triangle overlap so that the circle cuts each side
of the triangle into 3 line segments.
What is the smallest possible perimeter of the triangle if the lengths
of the 9 line segments, the radius of the circle and the 3 equal
distances from the center to the sides are all integers?
Solved by: Ender Aktulga
Pyramid #1
A pyramid has a quadrilateral base ABCD, vertex V, and altitude VH.
What is the smallest such pyramid (in the sense that its longest
edge is as small as possible) such that its 8 edges and the line
segments AH, BH, CH, DH and VH all have distinct integer lengths?
Solved by: Jean Jacquelin, P.M.A. Hakeem, Ahmet Saracoglu
Pyramid #2
A pyramid has a quadrilateral base ABCD, vertex V, and altitude VH,
where H is the intersection of AC and BD.
What is the smallest such pyramid (in the sense that its longest
edge is as small as possible) such that its 8 edges and the line
segments AH, BH, CH, DH and VH all have distinct integer lengths?
Solved by: Jean Jacquelin, P.M.A. Hakeem, Ahmet Saracoglu
Deformed Cube
Imagine that a cube has been deformed so that it still has 6 planar
quadrilateral faces, 8 vertices, and 12 straight edges, but that
the 12 edges all have distinct integer lengths.
What is the shortest possible length for the longest edge?
* 99 Rods #1
(contributed by Denis Borris )
You are given 99 thin rigid rods with lengths 1, 2, 3, ..., 99.
You are asked to assemble these into as many right triangles as
you wish. What is the largest total area that can be obtained?
(Each side of a triangle must be one entire rod.)
Solved by: Lee Morgenstern, P.M.A. Hakeem, Paul Cleary, Ahsen Canat,
Ender Aktulga
* 99 Rods #2
(contributed by Denis Borris )
You are given 99 thin rigid rods with lengths 1, 2, 3, ..., 99.
You are asked to assemble these into as many triangles as you wish,
each having an integer area. What is the largest total area
that can be obtained? (Each side of a triangle must be one entire rod.)
Solved by: Lee Morgenstern, P.M.A. Hakeem, Paul Cleary, Ahsen Canat
* 99 Rods #3
Repeat problem #1, but a rod may be shared by two right triangles.
For example, you could have a 3,4,5 right triangle
and a 5,12,13 right triangle sharing the rod of length 5.
Your solution must lie flat in the plane without crossings or overlaps.
The objective is to cover the largest possible total area.
Each side of a triangle must be one entire rod.
Solved by: Lee Morgenstern, P.M.A. Hakeem
* 99 Rods #4
Repeat problem #2, but a rod may be shared by two integer triangles.
For example, you could have a 13,14,15 integer triangle
and a 9,12,15 right triangle sharing the rod of length 15.
Your solution must lie flat in the plane without crossings or overlaps.
The objective is to cover the largest possible total area.
Each side of a triangle must be one entire rod.
Solved by: Lee Morgenstern
99 Rods #5
You are given 99 thin rigid rods with lengths 1, 2, 3, ..., 99.
You are asked to assemble some or all of them into a plane figure enclosing
the largest possible total area. Rods may be placed only horizontally
or vertically, and may meet only at their endpoints.
Solved by: P.M.A. Hakeem, Paul Cleary, Ahsen Canat, Claudio Baiocchi
Dissecting a Square
It is possible to dissect a square into dissimilar right triangles
(that is, so no two of the triangles are similar).
Find the smallest such square such that all of the triangles have
integer sides.
Solved by: Denis Borris, Fotos Fotiadis, Paul Cleary
4 Points on a Square
Let ABCD be a square, and let E, F, G and H be points on the 4 successive
sides of the square with the distances AE, EB, BF, FC, CG, GD, DH, HA
all integers. What is the smallest such square such that the
distances EF, EG, EH, FG, FH, GH are also integers?
Solved by: Andreas Abraham, Gaurav Agrawal, Denis Borris,
Fotos Fotiadis, P.M.A. Hakeem, Paul Cleary, Naim Uygun, Ender Aktulga
* 6 Points on a Circle
What is the smallest possible radius of a circle such that it is
possible to place 6 points on the circumference with an integer
distance between any two?
Solved by: Nick McGrath, Denis Borris, Fotos Fotiadis, Ahsen Canat
* 6 Points on a Circle #2
What is the smallest possible radius of a circle such that
it is possible to place 6 points on the circumference with
the 15 distances between the points being distinct integers?
Solved by: Ahsen Canat, Ahmet Saracoglu
* 6 Points on a Circle #3
(contributed by Denis Borris )
What is the smallest possible radius of a circle such that
it is possible to place 6 points on the circumference with
the radius, diameter, and the 15 distances between the points
being distinct integers?
Solved by: Ahsen Canat, Ahmet Saracoglu
4 Triangles
(contributed by Denis Borris )
Find 4 triangles with integer sides and the same integer area such that
2 of the triangles have 2 equal sides, and the other 2 triangles
also have 2 equal sides.
That is, A1B1=A2B2,
A1C1=A2C2,
A3B3=A4B4, and
A3C3=A4C4.
Find the set with the smallest area.
Solved by: Jean Jacquelin, Fotos Fotiadis, Paul Cleary,
P.M.A. Hakeem, Naim Uygun
* Inscribed Triangle #1
Let ABC be an arbitrary triangle, and L be an arbitrary line.
Is it always possible to find points D on AB, E on BC,
and F on AC such that triangle DEF is equilateral, and one of its sides
is parallel to L?
Solved by: Jean Jacquelin, Paul Cleary, Ionut-Zaharia Chirila
* Inscribed Triangle #2
Let ABC be an arbitrary triangle, with D a point on AB.
Under what circumstances is it possible to find points E on BC
and F on AC such that triangle DEF is equilateral?
Solved by: Jean Jacquelin
* Two Fields
(contributed by Denis Borris )
Farmer Brown has a triangular field with integer sides. Farmer Grey
has two square fields with integer sides (measured in meters). Both farmers
own the same amount of land (to within one square centimeter), and used
the same amount of fencing to enclose their fields. What is the minimum area
(in square meters) they could own?
[Note: the fields do not overlap or share sides.]
Solved by: Nick McGrath, Fotos Fotiadis, Paul Cleary, Mark Rickert,
P.M.A. Hakeem, Naim Uygun, Ender Aktulga
6 Brothers
The 6 Foodlemyer brothers hate each other with great passion. Today they
are on the parade ground, which is a 300-meter square. None of them wants
to be anywhere near any of the others. Where should they stand so that the
two closest are as far apart as possible?
Solved by: James Layland, Nick McGrath, Ritwik Chaudhuri,
Toby Gottfried, Andreas Abraham, Joshua Woodard, P.M.A. Hakeem, Paul Cleary,
Ender Aktulga
Big Belt
On Tralfamador they have constructed a new Information Superhighway,
a thin flexible belt around the planet's equator in a perfect circle
8,000 miles in diameter. Unfortunately, Foodlemyer Fabricators made the
belt 1 inch too long, so they have decided to place a circular disk
under the belt at one point to take up the slack.
How large should the disk be made?
Solved by: Carlos Rivera, Nick McGrath, Martin Rubin, Mark Rickert,
Paul Cleary, P.M.A. Hakeem, Ender Aktulga
Chords
(contributed by Sudipta Das)
Let O be the center of a circle and OR be a radius. Along OR mark off
points A1, A2, A3, ..., An.
Let the chord perpendicular to OR through Ai meet the circle
at Bi.
Find the smallest circle for which the distances OR, OAi,
AiBi, and BiR are all integers
for n=1 through n=8.
Solved by: Nick McGrath, Fotos Fotiadis, P.M.A. Hakeem, Paul Cleary
Shattern
(contributed by Sudipta Das )
Planet Shattern has installed a forcefield 300 miles
wide around the planet to ward off alien invasions.
This is a thin flat circular ring in the planet's equatorial plane.
Watch-towers have to be installed, at various
points on the planet, to guard the forcefield.
The authorities have decided to position the watch-towers at those locations
which offer the best view of the forcefield (i.e., those positions
where the field appears widest). The radius of the planet is 7500 miles
and the inner radius of the forcefield is 10200 miles.
What is the latitude of the watch-towers?
Solved by: Nick McGrath, Fotos Fotiadis, Gaurav Agrawal,
Andreas Abraham, Paul Cleary, Ender Aktulga
Circumscribe
(contributed by Nick McGrath )
Start with a unit circle. Circumscribe an equilateral triangle around it,
then another circle around that. Circumscribe a square around this circle,
and another circle around that. Continue with a regular pentagon, hexagon,
etc. Does the sequence of circles converge, and if so, what is the
limiting value of the radius?
Solved by: Sudipta Das, Gaurav Agrawal, Fotos Fotiadis, P.M.A. Hakeem,
Paul Cleary, Amogh Keni, Ender Aktulga, Ionut-Zaharia Chirila
Sum of Circles
(contributed by Nick McGrath )
Start with a unit square. Form an isosceles triangle from two vertices
and the midpoint of the opposite side. Inscribe a circle in this triangle.
Inscribe a second square in this circle, form a second isosceles triangle
as before, and so forth. What is the sum of the areas of all the circles?
Solved by: Fotos Fotiadis, Mark Rickert, P.M.A. Hakeem, Paul Cleary,
Amogh Keni, Ionut-Zaharia Chirila
Midpoints of Arcs
(contributed by Fotos Fotiadis)
Two circles intersect at points A and B. Draw a line through B
intersecting the two circles at C and D. N is the midpoint of
segment CD, P is the midpoint of arc AC and Q is the midpoint of
arc AD. Prove that the lines NP and NQ are perpendicular.
Solved by: Nikolai Dimitrov, George Kalampalikis, Ionut-Zaharia Chirila,
Emre Karabiyik, Amogh Keni
In A Square #1
(contributed by Ritwik Chaudhuri)
There is a point M inside a square ABCD such that angle MAB is
60° and angle MCD is 15°. Find angle MBC.
Solved by: Rakesh Kumar Banka, Fotos Z. Fotiadis, Sudipta Das,
Janaki Mahalingam, Gaurav Agrawal, Arijit Bhattacharyya, Mark Rickert,
Paul Cleary, P.M.A. Hakeem, Naim Uygun, Ionut-Zaharia Chirila, Kushal Khaitan,
Ender Aktulga, Ahmet Saracoglu, Tarun R.D.
* In A Square #2
(developed from an idea submitted by Sudipta Das)
There is a square ABCD and a point M in the square such that the distances
MA, MB, MC and MD are all integers. Three of these distances are
consecutive prime numbers (such as 5, 7, 11). What is the smallest possible
side of the square?
Solved by: Ritwik Chaudhuri, Nick McGrath (solved both versions),
Sudipta Das, Fotos Fotiadis, Paul Cleary, P.M.A. Hakeem, Ahsen Canat, Naim Uygun,
Arthur Vause, Ender Aktulga, Ahmet Saracoglu
What's the Angle?
(contributed by Nick McGrath )
Let ABC be an isosceles triangle with angle BAC=100°. From A draw AD
parallel to BC with AD = AB. What is angle ACD?
Solved by: Sudipta Das, Rakesh Kumar Banka, Janaki Mahalingam,
Gaurav Agrawal, Le My An, Arijit Bhattacharyya, Fotos Fotiadis,
Diptajit Bhattacharyya, Ritwik Chaudhuri, Mark Rickert, Paul Cleary,
P.M.A. Hakeem, Naim Uygun, Ionut-Zaharia Chirila, Amogh Keni, Kushal Khaitan,
Ender Aktulga, Emre Karabiyik, Abhay Menon
* Spider
(contributed by Nick McGrath )
There is a square ABCD with a spider at A and a fly at B. The fly starts
walking towards C, while the spider walks directly towards the fly.
If the spider walks N times as fast as the fly, and catches the fly at C,
what is the value of N? (Extra Credit: what is the equation of
the spider's path?)
Solved by: Sudipta Das, Gaurav Agrawal, Andreas Abraham, Paul Cleary
Extra credit: Paul Cleary
5 Circles
(contributed by Nick McGrath )
A, B and C are the integer radii of mutually tangent circles with A>B>C.
Circle D is the circumcircle of A, B and C. Circle E is the inscribed
circle of A, B and C.
Find A, B and C such that: (1) D is the smallest integer possible;
(2) D has the smallest value for which both D and E are integers.
Solved by: Jean Jacquelin, Mark Rickert, Paul Cleary, P.M.A. Hakeem
5 Spheres
Three solid unit spheres are placed mutually touching. Two identical
smaller spheres are placed so they each touch all of first 3 spheres,
and touch each other through the central gap. What is the radius of
those spheres?
Solved by: Nick McGrath, Fotos Fotiadis, Andreas Abraham,
Gaurav Agrawal, Mark Rickert, Paul Cleary, Claudio Baiocchi, Amogh Keni
TetraSpheres
Define a tetrasphere to be 4 equal spheres, each externally tangent to
the other 3. Nest two tetraspheres so that each sphere in the larger
tetrasphere is externally tangent to 3 spheres of the smaller tetrasphere.
What is the ratio between the radii of the larger and smaller spheres?
Solved by: Nick McGrath, Fotos Fotiadis, Gaurav Agrawal,
Timothy Cornelius, Joshua Woodard, Amogh Keni
* Steiner Point
The Steiner minimal point (also called the Torricelli point) in a triangle
is the point at which the sum of the distances to the 3 vertices is minimum.
Find a construction for the Steiner minimal point using only a compass.
Solved by: Jean Jacquelin, Fotos Fotiadis, Claudio Baiocchi
Trisection
(contributed by Ritwik Chaudhuri)
Let ABC be a triangle, with B a right angle. Let the trisectors of angle C
meet AB at D and E, with D closer to A. If AD is 50 and DE is 20, what is
the length of EB?
Solved by: Nick McGrath, Fotos Fotiadis, Sudipta Das, Gaurav Agrawal,
Andreas Abraham, Arijit Bhattacharyya, Mark Rickert, P.M.A. Hakeem, Paul Cleary,
Naim Uygun, Ionut-Zaharia Chirila, Claudio Baiocchi, Ender Aktulga, Amogh Keni
Tan Sum
(contributed by Nick McGrath )
Prove that tan(80) + tan(120) + tan(160) = tan(80) tan(120) tan(160)
Solved by: Ritwik Chaudhuri, Sudipta Das, Andreas Abraham,
Fotos Fotiadis, Gaurav Agrawal, Arijit Bhattacharyya, Diptajit Bhattacharyya,
P.M.A. Hakeem, Arthur Vause, Ionut-Zaharia Chirila, Naim Uygun, Amogh Keni,
Kushal Khaitan, Ender Aktulga, Tarun R.D.
* Block Box #1
Prove that it is not possible to fill a rectangular box with 2 or more
cubes, all of different sizes. (Note: the sizes are not restricted
to integers.)
Solved by: Nick McGrath, Lee Morgenstern
** Block Box #2
Is it possible to fill a rectangular box with 2 or more solid rectangular
blocks so that all the dimensions of all the blocks are different?
For example, you could not have two blocks whose dimensions are
A×B×C and A×D×E.
* Spheres
There are 4 solid spheres arranged so that each one is touching all
of the others. The 3 bottom spheres touch the flat floor at points
A, B and C. The top sphere has a radius of 12 centimeters. If it were
replaced by a sphere with radius 25 cm, then its center would be
14, 15 and 16 cm further from from points A, B and C, respectively.
What is the radius of each sphere?
Solved by: Nick McGrath (solved both the original and corrected
versions), Ahsen Canat
Brick
Find a rectangular solid where the 12 edges and both diagonals on all 6 faces
are integers.
** Extra Credit: Is it possible for the main diagonal to be integral
as well?
Solved by: James Layland, Matthew Ender, Gilles Ravat,
Hrishikesh Nene, Rahul Kelkar, Ritwik Chaudhuri, Sudipta Das, Janaki Mahalingam,
Gaurav Agrawal, Mark Rickert, Paul Cleary, P.M.A. Hakeem, Naim Uygun,
Claudio Baiocchi, Ionut-Zaharia Chirila, Ender Aktulga
 |
Send us an email to submit answers to these puzzles, to ask for help, or
to submit new puzzles.
Share your favorite puzzles with other puzzle-lovers.
Be sure to change the $ to an @ in our email address.
|
Quick Links
Copyright © 2024 The Contest Center
| | |




